NOTE: ARCADY 7 onwards provides options for the direct modelling of double roundabouts and other systems of linked roundabouts. This modelling uses approximate methods and is less rigorous than the empirically based core model of ARCADY, but, provides a convenient way to automate the suggestions given below which are aimed at users of previous versions.
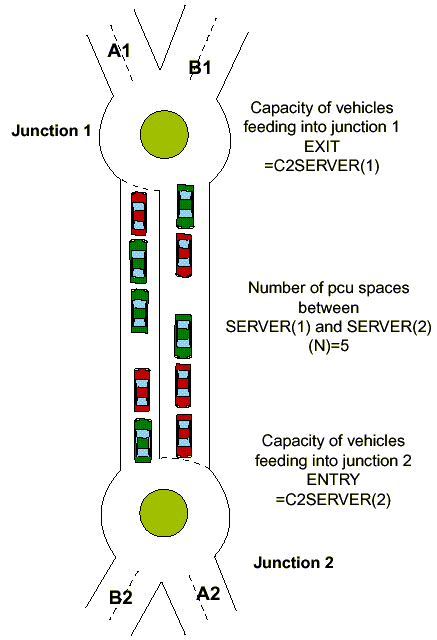
Each junction can be modelled separately but the models will always overestimate the capacity of the internal links (C1 and C2 in the diagram). Then there will be a knock-on effect on other traffic streams (A1, B1, A2, B2). The capacity of the internal give-way lines will always be less than that of a similar isolated junction, because the upstream junction creates “holes” in the traffic, and there will not always be vehicles at the give-way line able to take advantage of gaps in the priority traffic.
Having modelled two junctions independently, there is a method of calculating by what percentage (approximately) the capacity of the give-way line has been overestimated. Take, for example, the traffic flowing from Junction 1 to Junction 2. There are two sequential bottlenecks, C2SERVER(1) and C2SERVER(2) each with its own capacity. The “capacity” of the exit from Junction 1 is not related to exit geometry alone; it is simply the actual traffic flow down the exit (after negotiating the capacity restrictions of A1 and B1). The capacity of the give-way line, C2SERVER(2), can be obtained from the independent model of Junction 2 in isolation. Using standard queueing theory, the overall capacity of two sequential bottlenecks can be expressed as some proportion, P, of the capacity of the give-way line alone, where:
P = (R(N+2) – R) / (R(N+2) – 1)
where R is the ratio of the two individual capacities, C2SERVER(1) / C2SERVER(2)
and N is the number of pcus in the internal link (5 pcus in this example) (generally about 1 pcu per 10 metres)
If, for example, the capacity of the upstream bottleneck, C2SERVER(1) = 800 pcu/hour and the capacity of the give-way line,
C2SERVER(2) = 500 pcu/hour
then R = 800/500 = 1.6 ,
and N = 4 pcu (see diagram)
P = (1.66 – 1.6) / (1.66 – 1) = 15.177 / 15.777
so = 0.962
thus the overall capacity of the system
= 500 * 0.962 pcu/hour.
Having revised the capacity of the give-way line, you may find that the queue stretches back to beyond the upstream junction. This is a second type of interaction between two junctions, which the above method does not take into account. You need to study mean queues and queue variability to see if it occurs, but the effect of blocking-back is too random to be capable of a mathematical solution. You have to either manually “guesstimate” the effect or, better still, design the internal links with enough storage capacity to prevent the problem occurring.
How to obtain the values of C2SERVER(1) and the similar C2SERVER(2).
This article says that the value is “simply the actual traffic flow down the exit…” and is likely to be written in response to a real user’s enquiry and as such the solution works for that particular situation but not all, i.e. the article is not ‘general’ enough. EG. The capacity of the Junction 1 ‘bottleneck’ I.e. C2SERVER(1) is the actual traffic flow down the exit, only when there is significant queueing on both A1 and B1. If, for example there was no traffic on arms A1 and B1 the traffic flow on the exit would be near zero and would obviously not represent the capacity of the situation. I have suggested that the entries should be loaded with sufficient entry flows to establish sizeable queues on all entries and that the combined capacities can then be summed to provide a value. Said another way: if the upstream links have a demand flow that does not make full use of the available capacity the downstream links will have capacities which relate to the upstream demand, and as such cannot be summed to get a value for C2SERVER(1). This is because the upstream demand determines the downstream capacities. Note however, that if the combined capacities of the upstream links exceed those expected of the connecting exit link then you have just proved that the need for any capacity adjustment of the downstream entry is probably unnecessary.
Caveat
Please note that this suggested solution has not been subjected to the same rigorous validation that is associated with those features built into ARCADY itself.